linear vs. exponenziell

Die österreichischen Qualitätsmedien überschlagen sich in Didaktik. Da wird erklärt, in Grafiken gezeigt, in Videos veranschaulicht, wie das Wachstum des Coronavirus funktioniert. Der österreichische Bildungsminister glaubt noch an „lineares“ Wachstum: jeden Tag gleich viele Fälle mehr:
100 – 140 – 180 – 220 – 260 – 300 …

Er wird belehrt: nein, es sei exponenziell: jeden Tag den gleichen Prozentsatz mehr … derzeit ungefähr 40% pro Tag Zunahme. Also z.B.
100 – 140 – 196 – 274 – 384 – 538 …
letztlich viel schneller als linear.

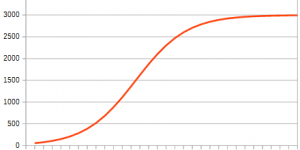
[Die Grafik zeigt die Zunahme der Coronavirus-Infektion für ganz Österreich zwischen 6.3. und 15.3. rot sind die realen Daten, gelb ist eine lineare Modellierung zwischen den beiden Freitagen 6.3. und 13.3., grün ist eine exponenzielle Modellierung zwischen diesen beiden Tagen. Die Grafik zeigt, wie grandios naiv die Annahme von Linearität ist und wie schnell da exponenzielles Wachstum ganz gut zur Realität passt. Der Zeitraum zwischen 6.3. und 13.3. war von einem prozentuellen Wachstum von durchschnittlich ca. 37% pro Tag geprägt.]

Der Standard (Ausgabe 14./15.3., Agenda Coronavirus, S. 11) zeigt Wachstumskurven aus verschiedenen Ländern. Steiler, weniger steil, auch schwach dahindümpelnd: durchaus verschiedene. Gemeinsam ist ihnen: Wachstum.

Mathematische Modelle sind oft sehr vereinfacht und geben die Wirklichkeit nur eingeschränkt wieder. Und sowohl lineares als auch exponenzielles Wachstum kennen keine „Politik“: sie schließen Veränderungen durch äußere Einflussnahme wie Politik völlig aus. Sowohl lineares als auch exponenzielles Wachstum sind „mechanistische“ Modelle.

[Exakt bis hierher reicht übrigens im Normalfall der mathematische Maturastoff. Ab jetzt geht es über normalen Maturastoff hinaus.]

Nein, so einfach ist es nicht. Biologisches Wachstum ist nicht mechanisch. Es hängt von durchaus veränderbaren Faktoren und letztlich auch von Zufällen ab.

Logistisches Wachstum

Zunächst brauchen wir noch ein weiteres „mechanistisches Wachstumsmodell“: logistisches Wachstum. Es ist eine Weiterentwicklung des exponenziellen Modells.

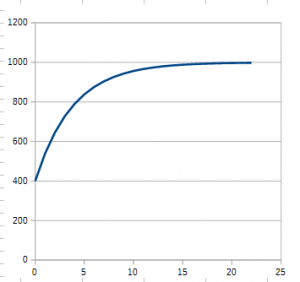
Im exponenziellen Wachstum hängt die Wachstumsrate von der Anzahl der bereits vorhandenen Individuen ab. Je mehr Personen infiziert sind, desto mehr können die Infektion weitergeben, desto stärker wächst die Zahl der Infizierten. Diese Grundannahme ist zunächst vernünftig. Zwei Erkrankte können die Infektion doppelt so schnell weitergeben wie ein Erkrankter. Das führt zu den zunächst scheinbar harmlos „flach“, dann aber plötzlich steil emporschießenden exponenziellen Wachstumskurven. Man kann das Modell durch eine Differenzialgleichung beschreiben: y‘, die Veränderungsrate, das Wachstum ist vom Bestand y abhängig:

Exponenzialfunktionen sind die Lösung; das sieht dann so aus:

wobei das c einfach der „Startwert“ der Beobachtung ist (c = y(0) und a der Wachstumsfaktor ist. a = 1,37 würde z.B. ein Wachstum von 37% pro Beobachtungseinheit bedeuten.)

Aber Exponenzialfunktionen funktionieren nie langfristig in einer Realität. Wenn sich pro Woche auf einem Teich die Zahl der Seerosen verdoppelt, ist das exponenziell: dann ist eine Woche, bevor der Teich voll ist, der Teich halb voll. Und eine Woche später wäre er voll und es ginge gar nichts mehr. Schon davor gehts nicht mehr. Für Infektionen: Wenn alle (infizierbaren) Bewohner infiziert sind, gibt es keine neuen Infektionen mehr.

Wachstum ist letztlich auch abhängig von der Zahl der Infizierbaren. Je mehr Menschen infizierbar sind, desto stärker das Wachstum. Je weniger infizierbar sind (also: je mehr schon infiziert sind), desto schwächer das Wachstum. Wenn wir mit L das Limit, die obere Grenze aller Infizierbaren bezeichnen, ist die beschreibende Differenzialgleichung

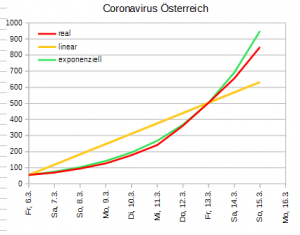
Das liefert „beschränktes“ Wachstum: Kurven, die gegen die obere Grenze L hin wachsen und dieser Grenze immer näher kommen – aber sie nicht überschreiten. Die Funktionsgleichung könnte man hinschreiben mit

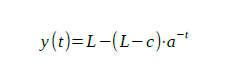und die Funktionsdiagramme sehen ungefähr so aus:

Und nachdem beides stimmt: je mehr Infizierte, desto stärker das Wachstum, je weniger Infizierbare, desto schwächer das Wachstum, entsteht die Differenzialgleichung

und wir bekommen Kurven, die zunächst quasi-exponenziell harmlos beginnen, dann in überschießendes immer-steileres Wachstum übergehen, dann eine Zeitlang beinahe linear erscheinen (das sah der Bildungsminister) und schließlich in ein fast „friedliches“ beschränktes Wachstum übergehen. So sehen sie typischerweise aus:

So eine Kurve kann man sehr gut erkennen, wenn man das Wachstum des Coronavirus in China ansieht. Es ist exponenziell explodiert, hat sich dann scheinbar „linear“ etwas derfangen und hat sich nun bei gut 80.000 Fällen insgesamt beruhigt. Es kommt praktisch nix mehr dazu.

Das ist das logistische Modell. Es stimmt letztlich zu sehr vielen biologischen Wachstumsvorgängen. Wir in Europa sind „nach“ China und noch in der exponenziellen Phase.

Wenn man naiv oder zynisch oder beides wäre, könnte man sagen: wurscht, was wir tun: wenn genügend krank sind, wird sich das alles eh einpendeln.

Das logistische Modell ist gut; es ist viel weniger naiv als das von den Qualitätsmedien derzeit noch so breit erklärte exponenzielle Modell: aber es ist immer noch mechanistisch. Es kennt keinen Einfluss von Politik.

[Nebenbemerkung: alle 3 hier behandelten mathematischen Modelle basieren auf dem Kontinuum, auf den reellen Zahlen. Für Anzahlen (von Viren, von infizierten Personen, von Genesungs- oder Sterbefällen) sind sie an sich, vom theoretischen Ansatz nicht geeignet. Sie liefern keine ganzzahligen Ergebnisse. Infektionen „springen“; sie treten nicht in Dezimalzahlen auf. Um Wirklichkeit wirklich zu modellieren, fehlt noch etwas Wesentliches: Stochastik. Wahrscheinlichkeit; Statistik.]

Politischer Einfluss

Die österreichische Bundesregierung versucht, die Rate der prozentuellen Zunahme zu senken: durch radikale Maßnahmen wie das breite Einschränken von Sozialkontakten. Ja, es macht schon einen Unterschied aus, ob pro Tag 40% oder nur 20% oder gar nur 10% dazu kommen. (Auf heute und auf gestern waren es nur mehr etwa 30%.) Die Bundesregierung versucht damit, den Punkt der real höchsten Erkranktenanzahl hinauszuschieben – nicht so sehr, um die Gesamtzahl der Erkrankungen zu reduzieren, sondern die Anzahl der Kranken pro Zeitabschnitt. Die Anzahl der ernstlich Erkrankten soll immer unter dem bleiben, was das Gesundheitssystem zu leisten im Stande ist.

Die Anzahl der Erkrankungen insgesamt würde sich damit noch nicht reduzieren; sie würde sich nur auf einen deutlich längeren Zeitraum verteilen. Damit wäre sie ein weit kleineres Problem für das Gesundheitssystem. (Und es gäbe die Hoffnung auf Medikamente.) Dieser Ansatz ist an sich vernünftig: Die Katastrophe akzeptieren, aber besser verteilen.

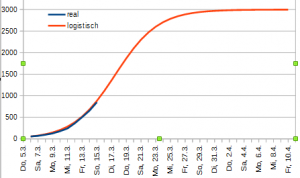
Auch die vorliegenden scheinbar noch exponenziell wachsenden Daten lassen sich gut in eine logistische Kurve einpassen. Das folgende Diagramm beschreibt eine logistische Kurve, deren blauer Teil die konkreten Infektionsdaten Österreichs beschreibt und deren roter Teil ein logistisches Wachstum gegen 3.000 Infektionen darstellt. Ja: so könnte das kommen. Ja, in etwa so schnell und so bald:

Es sind mehrere Modellierungen auf der Basis der momentan vorhandenen Daten möglich. Auch mit geringeren Obergrenzen, auch mit höheren Obergrenzen. Auch in längeren Zeiträumen. Die Sache ist noch nicht ausgemacht. In China hat sich eine Obergrenze von etwa 85.000 herausgestellt. Das kann man sicher nicht proportional auf Österreich übertragen. Bei uns wird sie viel tiefer liegen. Dass Italien so katastrophal betroffen ist, liegt u.a. auch daran, dass dort viel weniger Intensivbetten zur Verfügung standen wie in anderen vergleichbaren Ländern.

Aber es wäre m.E. mehr Politik möglich und weniger Angst nötig. Ein wesentlicher Parameter des logistischen Wachstums ist die Obergrenze L. Das ist die Anzahl der im Prinzip Infizierbaren. Die nimmt mit der Infektion ab: wer infiziert ist, ist nicht mehr infizierbar. Aber auch: wer ein gesundes Immunsystem hat, ist nicht (so ohne Weiteres) infizierbar. Wer über Infektionswege etwas weiß, kann sich schützen und ist nicht so gut infizierbar. Eine Impfung würde die Anzahl der Infizierbaren vermindern.

Die Arbeit an L kommt m.E. derzeit zu kurz. Man versucht hauptsächlich, die Infektionskurve zu stauchen und zu verlängern. Verschiedene Kurven verschiedener Länder zeigen aber, …
1. dass das logistische Modell als Grundmodell eigentlich ganz gut passt und
2. dass Politik möglich ist, über das Verzögern des Wachstumsprozesses hinaus.

Wir könnten den (österreichischen) Menschen erklären, wie sie ihr Immunsystem fit oder wenigstens fitter als jetzt kriegen können.